
Solving System of Equations Using Graphical Method Multiplying Eqn(1) by 2 and Eqn(2) by 3, we get The coefficients of y are 3 and 2 LCM (3, 2) = 6 Using the elimination method to solve the system of equations, we eliminate one of the unknowns, by multiplying equations by suitable numbers, so as the coefficients of one of the variables become the same. Solving System of Equations Using Elimination Method Hence, x = 9 and y = 4 is the solution of given system of equations. Solving System of Equations Using Substitution Methodįor solving the system of equations using the substitution method given two linear equations in x and y, express y in terms x in one of the equations and then substitute it in 2nd equation. Let us understand 3 ways to solve a system of equations given the equations are linear equations in two variables. Similarly, for solving a system of equations in 3 variables, we will require at least 3 equations. To solve a system of equations in 2 variables, we need at least 2 equations. Infinite Many SolutionsĪ system of equations can have infinitely many solutions when there exists a solution set of infinite points for which L.H.S and R.H.S of an equation become equal, or in the graph straight lines overlap each other.Īny system of equations can be solved in different methods. No SolutionĪ system of equations has no solution when there exists no point where lines intersect each other or the graphs of equations are parallel. Similarly, for a system of linear equations in two variables, the unique solution is an ordered pair (x, y) which will satisfy both the equations in the system. Let understand the concept of a unique solution using a linear equation in one variable, 4x = 8 has a unique solution x = 2 for which the L.H.S is equal to the R.H.S. The unique solution of a system of equations means that there exists only one value for the variable or the point of intersection of the lines representing those equations, on substituting which, L.H.S and R.H.S of all the given equations in the system become equal.įor example, we know that a linear equation in one variable will always have one solution.

There can be different types of solutions to a given system of equations,

The main reason behind solving an equation system is to find the value of the variable that satisfies the condition of all the given equations true. We compute the values of the unknown variables still balancing the equations on both sides. įor each solution ( c 0, s 0) of this system, there is a unique solution x of the equation such that 0 ≤ x < 2 π.Solving a system of equations means finding the values of the variables used in the set of equations. The numerous singular points of the Barth sextic are the solutions of a polynomial systemĪ very simple example of a system of polynomial equations is For the case of solutions of which all components are integers or rational numbers, see Diophantine equation. Searching for solutions that belong to a specific set is a problem which is generally much more difficult, and is outside the scope of this article, except for the case of the solutions in a given finite field. As these methods are designed for being implemented in a computer, emphasis is given on fields k in which computation (including equality testing) is easy and efficient, that is the field of rational numbers and finite fields.
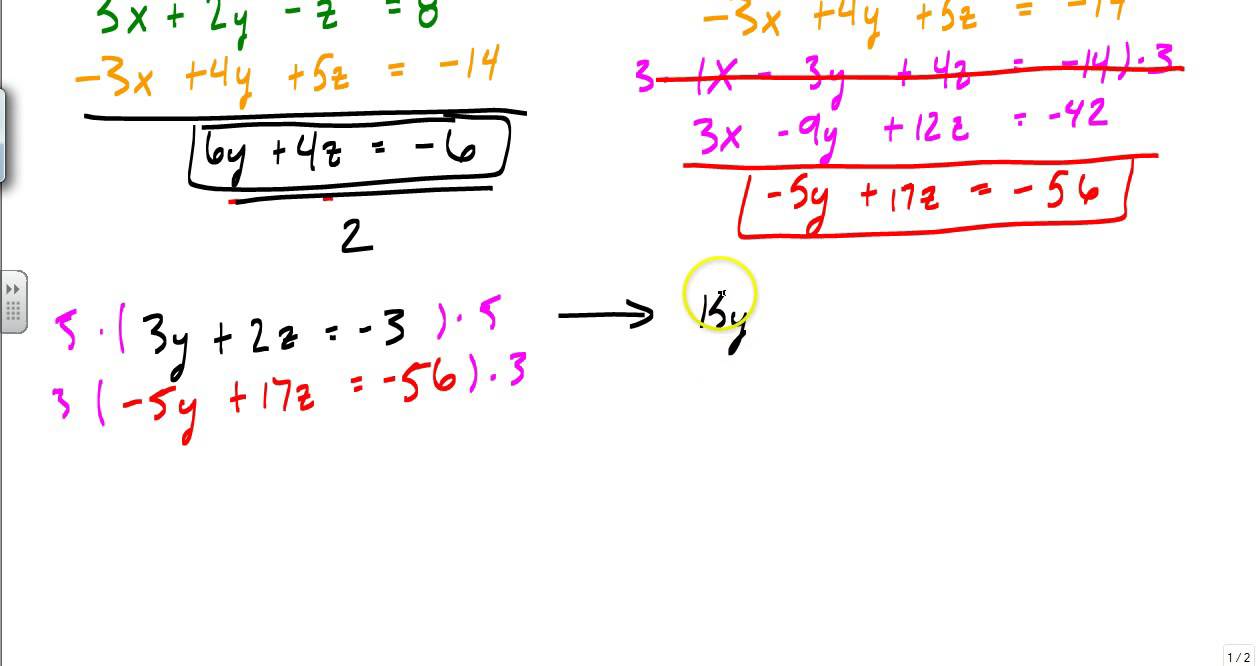
This article is about the methods for solving, that is, finding all solutions or describing them. When k is the field of rational numbers, K is generally assumed to be the field of complex numbers, because each solution belongs to a field extension of k, which is isomorphic to a subfield of the complex numbers. , x n, over some field k.Ī solution of a polynomial system is a set of values for the x is which belong to some algebraically closed field extension K of k, and make all equations true. , f h = 0 where the f i are polynomials in several variables, say x 1. Root-finding algorithms for common roots of several multivariate polynomialsĪ system of polynomial equations (sometimes simply a polynomial system) is a set of simultaneous equations f 1 = 0.


 0 kommentar(er)
0 kommentar(er)
